Дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке O, а прямые AB и CD - в точке K. Прямая KO пересекает стороны BC и AD в точках M и N соответственно, а угол BAD равен 30°. Известно, что в трапеции ABMN и NMCD можно вписать окружность. Найти отношение площадей треугольника BKC и трапеции ABCD.
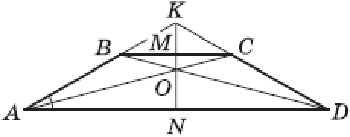
Как известно, для произвольной трапеции прямая, соединяющая точку пересечения диагоналей и точку пересечения продолжений боковых сторон, делит каждое из оснований пополам. Итак, BM = MC и AN = ND. Далее, так как в трапеции ABMN и NMCD можно вписать окружность, то
BM + AN = AB + MN,
MC + ND = CD + MN.
Отсюда следует, что AB = CD, то есть трапеция ABCD — равнобокая. Искомое отношение площадей не зависит от масштаба, поэтому мы можем принять, что KN = x, KM = 1.
Из прямоугольных треугольников AKN и BKM получаем, что \( AK=2x, AN=3\sqrt{x},\;\; BK=2, BM=\sqrt3 \)
Записывая вновь уже использованное выше соотношение
BM + AN = AB + MN \( \Leftrightarrow \sqrt3 + x\sqrt3=(2x-2)+(x-1), \)
находим
\( x=\frac{3+\sqrt3}{3-\sqrt3}\)
Нам требуется вычислить отношение:
$$ \frac{S_{\Delta BKC}}{S_{ABCD}}=\frac{S_{\Delta BKC}}{S_{\Delta AKD}-S_{\Delta BKC}}=\\=\frac{1}{\frac{S_{\Delta AKD}}{S_{\Delta BKC}}-1}=\frac{1}{x^2 -1}=\\=\frac{1}{(\frac{3+\sqrt3}{3-\sqrt3})^2 -1}=\frac{(3-\sqrt3)^2}{12\sqrt3}=\frac{2\sqrt3 -3}{6} $$Здесь мы использовали тот факт, что площади треугольников AKD и BKC относятся как квадраты сторон KN и KM, то есть как x2.
Ответ:\(\frac{2\sqrt3 -3}{6}\)