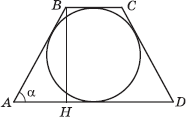
Пусть ABCD - данная равнобочная трапеция с основаниями AD и BC, пусть BH - высота этой трапеции, опущенная из вершины B.

Так как в данную трапецию можно вписать окружность, то \( AB+CD=BC+AD=\frac{p}{2}\),

следовательно, \( AB=CD=\frac{p}{4} \)

Из прямоугольного треугольника ABH находим,

$$ BH=AB\cdot sin\angle BAD \Leftrightarrow 2r=\frac{p sin\alpha}{4} \Leftrightarrow r=\frac{p sin\alpha}{8} $$

Ответ: \( \frac{p sin\alpha}{8} \)