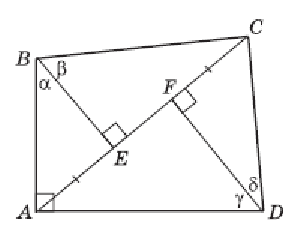
Доказательство. Так как угол A равен 90°, а угол C не превосходит 90°, то точки E и F лежат на диагонали AC.

Без ограничения общности мы можем считать, что AE < AF (в противном случае следует повторить все нижеследующие рассуждения с заменой точек B и D).

Пусть ∠ABE =α, ∠EBC = β, ∠FDA = γ, ∠FDC = δ. Нам достаточно доказать, что \(\alpha + \beta + \gamma + \delta = \pi\). Так как

$$ \frac{\pi}{2}=\angle BAD = \angle BAE + \angle FAD = (\frac{\pi}{2}-\alpha)+(\frac{\pi}{2}-\gamma) =\\=\pi-\alpha-\gamma, $$

то \( \alpha+\gamma=\frac{\pi}{2} \) и в частности tgγ tgα = 1.

Далее, имеем:

$$ tg \beta tg \delta=\frac{CE}{BE}\cdot\frac{CF}{DF}=\frac{AF}{BE}\cdot\frac{AE}{DF}=\\=\frac{AF}{DF}\cdot\frac{AE}{BE}=tg \gamma tg \alpha = 1, $$

откуда получаем, что \( \beta+\delta=\frac{\pi}{2}\), что и требовалось доказать.