Поскольку боковые ребра четырехугольной пирамиды равны между собой, ее вершина Е проектируется в точку О - центр прямоугольника ABCD. С другой стороны, из равенства ребер треугольной пирамиды следует, что все ее вершины основания лежат на окружности с центром в точке О.

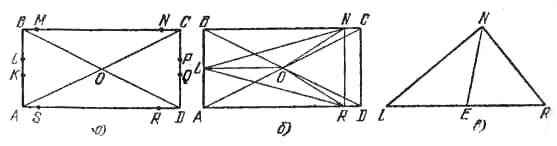
Пусть окружность, на которой лежат вершины основания треугольной пирамиды, пересекает стороны прямоугольника ABCD в точках, обозначения которых даны на рис. а. Из того, что боковые грани треугольной пирамиды - равнобедренные равновеликие треугольники, следует, что углы при вершинах этих треугольников либо равны, либо дополняют друг друга до 180°. Значит в основании лежит равнобедренный треугольник. (Докажите, что он не может быть правильным.) Далее, две вершины этого треугольника не могут находиться на меньших сторонах прямоугольника ABCD. Если основанием будет ΔLNS, то |SL| = |LN|, ∠SLN = 90°, а отсюда будет следовать, что ABCD - квадрат. Если же основанием будет ΔLNR, то из условия а < 60° будет следовать, что |BN| > |NR|. Значит, равными будут стороны RL и LN, что возможно, когда точки К и L совпадают с серединой АВ.

Рассуждая аналогично, придем к еще одной возможности: вершины основания треугольной пирамиды находятся в точках R, N и Р, при этом Р есть середина CD.

Рассмотрим первый случай (рис. б). Пусть |LO| = |ON| = |OR| = r. Тогда |NR| = |CD| = 2r tg\(\frac{\alpha}{2}\). Но, поскольку ∠LEN + ∠NER = 180°, треугольники LNE и NER, будучи приложенными друг к другу (см. рис. в), образуют прямоугольный ΔLNR. Значит,

$$ |LN|=\sqrt{4|LE|^2 - |NR|^2} = \sqrt{4h^2+4r^2-4r^2tg^2\frac{\alpha}{2}} $$

С другой стороны,

$$ |LN|^2 =(r+r\sqrt{1-tg^2\frac{\alpha}{2}})^2 + r^2tg^2\frac{\alpha}{2} $$

Таким образом,

$$ r^2 = \frac{2h^2}{2tg^2\frac{\alpha}{2}+\sqrt{1-tg^2\frac{\alpha}{2}} -1)} $$

Применяя аналогичные рассуждения к ΔNRP, получим, что r² < 0

Ответ: \(\frac{8h^3tg\frac{\alpha}{2}}{3(2tg^2\frac{\alpha}{2}+\sqrt{1-tg^2\frac{\alpha}{2}} -1)}\)