Пусть К - проекция вершины S на плоскость ABCD, L, М, N и Р - проекции S на стороны АВ, ВС, CD и DA.

Из условия следует, что треугольники LSN и MSP - прямоугольные с прямыми углами при вершине S.

Следовательно,

$$ |LK| • |KN| = |МК| • |КР| = |KS|^2 $$

А поскольку

$$ |LK| + |KN| = |МК| + |КР| = a, $$

возможны два случая: или |LK| = |КМ|, |КР| = |KN|, или |LK| = |КР|, |МК| = |KN|, т. е. точка К расположена на какой-то из диагоналей АС или BD, Разберем оба случая.

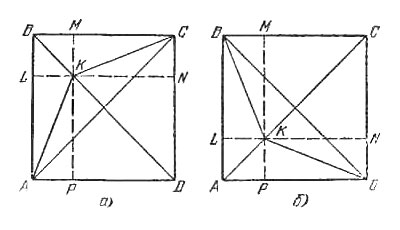
1. К - на диагонали BD (рис., а). На этом рисунке изображена проекция пирамиды на плоскость ABCD. Точка S находится «над» К). Обозначим |LK| = |КМ| = x. Теперь найдем:
   $$ |KS| = \sqrt{|LK|\cdot |KN|} = \sqrt{x(a-x)},\\ |SL|=\sqrt{|LK|^2+|KS|^2}=\sqrt{ax}. \\ S_{ABS}=\frac{a\sqrt{ax}}{2} $$

   Аналогично \(S_{ADS}=\frac{a\sqrt{a(a-x)}}{2}\). Далее,

   $$ V_{ABDS} = \frac{1}{6}a^2\sqrt{x(a-x)} $$

   С другой стороны, есть формула для объема тетраэдра: \(V=\frac{2SPsin\alpha}{3a}\), где S и P - площади двух граней тетраэдра, a - длина их общего ребра, α - двугранный угол между ними. По этой формуле имеем такое выражение:

   $$ V_{ABDS} = \frac{2}{3}\frac{S_{ABS}S_{BDS}sin\alpha}{|AK|} =\\= \frac{a^3\sqrt{x(a-x)}sin\alpha}{6\sqrt{(a-x)^2+x^2+x(a-x)}} $$

   Приравняв два выражения для V_ABDS, получим

   $$ x^2 - ax + a^2cos^2\alpha = 0 $$

   откуда

   $$ x(a-x) = a^2cos^2\alpha, \\ V_{ABCDS} = \frac{a^3|cos\alpha|}{3} $$

   Задача имеет решение, если |cosα| ≤ 1/2. Кроме того, угол при ребре AS тупой, поскольку плоскость ASM перпендикулярна грани ASD, а эта плоскость проходит внутри двугранного угла между плоскостями ASB и ASD. Следовательно, в 1-м случае задача имеет решение, если \(\frac{\pi}{2}\lt\alpha \leq \frac{2\pi}{3}\)

2. Точка К находится на диагонали АС (рис., б). Рассуждая так же, как в первом случае, получим (по-прежнему |LK| = x)
   $$ V_{ABDS}=\frac{a^2\sqrt{x(a-x)}}{6} = \frac{a^3xsin\alpha}{6\sqrt{x(a+x)}} $$

   откуда легко найдем х = а |cosα|,

   $$ V = \frac{a^3\sqrt{|cos\alpha|(1-|cos\alpha|)}}{6} $$

   Как и в 1-м случае, a > π/2. Таким образом, получаем:

   Ответ: если \(\frac{\pi}{2}\lt \alpha \leq \frac{2\pi}{3}\), возможны два ответа:

   $$ V_1 = -\frac{a^3cos\alpha}{6}, \;\;V_2=\frac{a^3\sqrt{-cos\alpha(1+cos\alpha)}}{6} $$

   если же \(\alpha \gt \frac{2\pi}{3},\;\;V=\frac{a^3\sqrt{-cos\alpha(1+cos\alpha)}}{6}\)