Пусть куб ABCDA₁B₁C₁D₁ поворачивается на угол α вокруг диагонали AС₁ (рис.).

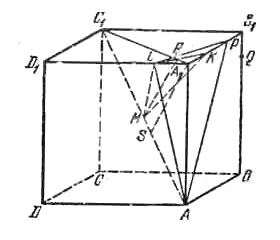
Возьмем на ребрах А₁В₁ и A₁D₁ точки К и L так, что |А₁К| = |А₁L| = х, опустим из K и L перпендикуляры на диагональ АС₁; ввиду симметрии куба относительно плоскости ACC₁A₁ эти перпендикуляры пройдут через одну точку М на диагонали АС₁. Пусть величина x выбрана таким образом, что ∠KML = α. Тогда после поворота вокруг диагонали AC₁ против часовой стрелки (если смотреть в направлении от А к С₁) на угол α точка К перейдет в L. Возьмем также на ребрах В₁А₁ и В₁В точки Р и Q на том же расстоянии x от вершины В₁. После того же поворота точка Q перейдет в Р. Следовательно, грань AВВ₁А₁ после поворота пройдет через точки А, L и Р и отсечет от нашего куба пирамиду АА₁РL, объем которой равен $\frac{1}{6}ax(a-x)$. Те же рассуждения верны для всех граней. Таким образом, объем общей части равен $a^3-ax(a-x)$. Нам осталось найти величину x из условия ∠КML = α. Для этого соединим М с серединой отрезка LK точкой R. Имеем

$$|MR| = x\frac{\sqrt2}{2}ctg\frac{\alpha}{2},\;\;\;|C_1R|=a\sqrt2 -x\frac{\sqrt2}{2}$$

и из подобия треугольников C₁RM и C₁A₁A найдем

$$x=\frac{2a}{1+\sqrt3ctg\frac{\alpha}{2}}$$

Таким образом, объем общей части равен

$$\frac{3a^3(1+ctg^2\frac{\alpha}{2})}{(1+\sqrt3ctg\frac{\alpha}{2})^2}$$