Пусть ребро правильного тетраэдра ABCD равно a, K и L - середины ребер CD и АB, (рис.).

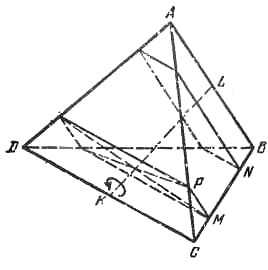
Возьмем на ребре СВ точку M, проведем через M сечение, перпендикулярное KL. Обозначим |CM| = x и определим величину x, при которой прямоугольник, получившийся в нашем сечении, будет иметь угол между диагоналями, равный α. Поскольку стороны получившегося прямоугольника равны x и a - x, величину x можно найти из уравнения:

$$ \frac{x}{a-x}=tg\frac{\alpha}{2},\;\;\;x=\frac{a tg\frac{\alpha}{2}}{1+tg\frac{\alpha}{2}} $$

Если мы возьмем на ребре ВС еще и точку N так, что |BN| = |СМ| = x, и проведем через нее сечение, перпендикулярное KL, мы получим второй прямоугольник с углом между диагоналями, равным α. Из этого следует, что плоскость BCD после поворота вокруг KL на угол α против часовой стрелки будет проходить через точки К, Р в N. Таким образом, после поворота плоскость BCD отсечет от тетраэдра ABCD пирамиду KPNC, объем которой равен

$$ \frac{|KC|}{|CD|}\cdot\frac{|CP|}{|CA|}\cdot\frac{|CN|}{|CB|}V_{ABCD}=\frac{x(a-x)}{2a^2}V=\\=\frac{tg\frac{\alpha}{2}}{2(1+tg\frac{\alpha}{2})^2}V $$

Те же рассуждения будут верны для любой грани тетраэдра. Следовательно, объем обшей части будет равен

$$ \frac{1+tg^2\frac{\alpha}{2}}{(1+tg\frac{\alpha}{2})^2}V $$