Внутри правильной треугольной пирамиды расположена вершина трехгранного угла, все плоские углы которого прямые, а биссектрисы плоских углов проходят через вершины основания. В каком отношении поверхность этого угла делит объем пирамиды, если каждая грань пирамиды разделена ею на две равновеликие части?
Пусть SABC - данная пирамида, SO - ее высота, G - вершина трехгранного угла. Из условия следует, что G находится на SO. Кроме того, грани трехгранного угла при пересечении с плоскостью основания АВС образуют правильный треугольник, стороны которого параллельны сторонам ΔАВС и проходят через его вершины.
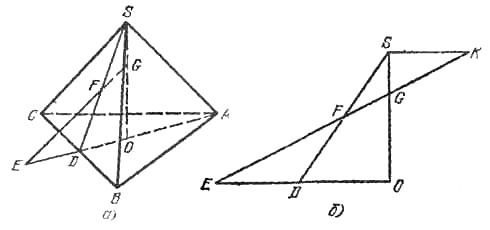
Следовательно, если одно из ребер трехгранного угла пересекает плоскость АВС в точке Е, а грань CSB - в точке F, то F лежит на апофеме SD боковой грани CSB и |ED| = |DA|.
По условию, |SF| = |FD|. Проведем через S прямую, параллельную ЕО, и обозначим через К точку пересечения этой прямой с прямой EF (рис. б). Имеем |SK| = |ED|. Значит,
$$ \frac{|SG|}{|GO|} = \frac{|SK|}{|EO|} = \frac{|ED|}{|EO|} = \frac{3}{4} $$Таким образом, объем пирамиды GABC составляет 4/7 объема пирамиды SABC.
С другой стороны, построенный трехгранный угол делит часть пирамиды SABC, расположенную над пирамидой GABC, пополам.
Ответ. Объем части пирамиды, расположенной вне трехгранного угла, к объему части внутри него относится как 3 : 11