Самая большая диагональ правильной шестиугольной призмы, имеющая длину d, составляет с боковым ребром призмы угол α. Определить объем призмы.
Из каждой вершины призмы, например из вершины А1 (рис.), можно провести три диагонали (A1E, A1D, A1C).
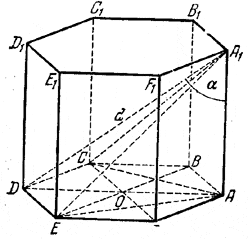
Они проектируются на плоскость ABCDEF диагоналями основания (АЕ, AD, АС). Из наклонных A1E, A1D, A1C наибольшая та, у которой проекция - самая большая. Следовательно, наибольшая из трех взятых диагоналей есть A1D (в призме есть еще диагонали, равные A1D, но больших нет).
Из треугольника A1AD, где ∠DA1A = α и A1D = d, находим H=AA1 = d cos α ,
AD = d sin α .
Площадь равностороннего треугольника АОВ равна 1/4• АО2 • √3. Следовательно,
Socн.= 6 •1/4• АО2 • √3 = 6 •1/4• ( АD/2 )2 • √3.
Объем V = S•H = 3√3/8 • АD2 • АA1
Ответ: 3√3/8 d3 sin2 α cos α .
Замечание. Для изображения правильного шестиугольника (основания призмы) можно построить произвольный параллелограмм BCDO. Откладывая на продолжениях прямых DO, CO, ВО отрезки OA = OD, OF= OC и ОЕ= ОВ, получаем шестиугольник ABCDEF. Точка О изображает центр.