Обозначим через М и N точки касания с шаром касательных, проведенных из А и В, М₁ и N₁ - проекции точек М и N на плоскость АВС (рис.).

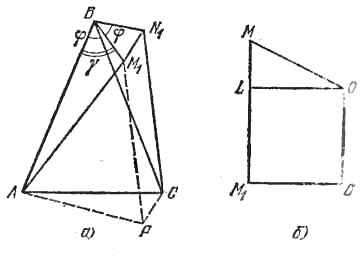
На рисунке изображены один из двух эквивалентных случаев расположения касательных, при которых эти касательные скрещиваются, в двух других случаях эти касательные лежат в одной плоскости. Можно найти: |АМ| = |CN| = l, |ММ₁| = |NN₁| = l sinα, |AM₁| = |CN₁| = l cosα. Найдем |BM₁| и |BN₁|.

На рис. б: О - центр шара, OL || ВM₁

$$ |BN_1| = |BM_1| = |OL| = \sqrt{r^2-(l sin\alpha - r)^2} =\\=\sqrt{2rl sin\alpha - l^2sin^2\alpha} $$

При повороте вокруг точки В на угол φ = ∠АВС точка А перейдет в С, М₁ - в N₁ следовательно, треугольники BM₁N₁ и ВАС подобны,

$$ |MN| = |M_1N_1| = |BM_1|\frac{|AC|}{|AB|}=\frac{2a}{l}\sqrt{2rl sin\alpha - l^2sin^2\alpha} $$

ΔM₁BN₁ получается из ΔАВС поворотом вокруг В на угол γ = ∠АВМ₁ с последующей гомотетией. Следовательно, угол между M₁N₁ и АС равен γ, а поскольку М₁N₁ и MN параллельны, угол между MN и АС - также γ.

Из ΔВМ₁А найдем

$$ cos\gamma = \frac{2rl sin\alpha - l^2sin^2\alpha + l^2 - l^2cos^2\alpha}{2l\sqrt{2rl sin\alpha - l^2sin^2\alpha}} =\\= \frac{r sin\alpha}{\sqrt{2rl sin\alpha - l^2sin^2\alpha}} $$

Затем

$$ sin\gamma = \frac{\sqrt{2rl sin\alpha - (l^2+r^2)sin^2\alpha}}{\sqrt{2rl sin\alpha - l^2sin^2\alpha}} $$

Найдем, используя полученные значения для |MN|, |ММ₁| и sinγ, объем пирамиды ACMN

$$ V_{ACMN}=\frac{1}{6}|AC|\cdot|MN|\cdot|MM_1|sin\gamma =\\= \frac{2a^2sin\alpha}{3}\sqrt{2rl sin\alpha - (l^2 +r^2)sin^2\alpha} \;\;\;\;\;\;(1) $$

Возьмем теперь точку Р так, что M₁N₁CP - параллелограмм, значит, MNCP - также параллелограмм. Пусть β - угол между AM и CN, тогда β = ∠AMР. Но ΔАВМ₁ получается из ΔCBN₁ поворотом вокруг В по часовой стрелке на угол φ = ∠АВС. Отсюда следует, что угол между АМ₁ и CN₁ равен φ, а, значит, и ∠АМ₁Р = φ, т.е. треугольники АМ₁Р и АВС подобны. Из этого подобия найдем |АР| = 2a cosα. Угол β равен углу ∠АМР, ΔАМР - равнобедренный, в котором |AM| = |МР| = l, |АР| = 2а cosα. Следовательно,

$$ sin\frac{\beta}{2}=\frac{a cos\alpha}{l}, \\ sib\beta=2sin\frac{\beta}{2}cos\frac{\beta}{2} = \frac{2a cos\alpha\sqrt{l^2-a^2cos^2\alpha}}{l^2} $$

Выразим объем пирамиды ACMN по-другому,

$$ V_{ACMN} = \frac{1}{6}|AM|\cdot|CN|x sin\beta = \frac{1}{3}ax cos\alpha\sqrt{l^2-a^2cos^2\alpha} $$

где x - искомое расстояние. Сравнивая эту формулу с равенством (1) получим $$ x = \frac{2a tg\alpha\sqrt{2rlsin\alpha - (l^2+r^2)sin^2\alpha}}{\sqrt{l^2-a^2cos^2\alpha}} $$