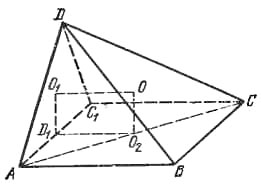
Возьмем С₁ так, что ABCC₁, - прямоугольник. D₁ - середина АС₁, О₁, O₂ - соответственно центры окружностей, описанных около треугольников АС₁D, АВС, О - центр сферы, описанной около ABCD. Очевидно, O₂ - середина АС, АВ и С₁С перпендикулярны AD и АС₁, следовательно, плоскости ADС₁ и АВСС₁ перпендикулярны, а O₁D₁O₂O - прямоугольник.

Таким образом, \(|DC_1| = \sqrt{|DC|^2 - |C_1C|^2}=\sqrt{b^2-a^2}\), радиус окружности, описанной около \(\Delta DC_1A\), будет равен

$$ R_1 =\frac{|DC_1|}{2sin\widehat{DAC_1}}=\frac{\sqrt{b^2-a^2}}{2sin\alpha} $$

А радиус сферы R = |OA| можно найти из прямоугольного треугольника AO₁O (на рисунке этот треугольник не изображен):

$$ R=\sqrt{|AO_1|^2 + |O_1O|^2} = \frac{1}{2}\sqrt{b^2 -a^2cos^2\alpha} $$