Пусть К - середина ребра АВ куба ABCDA₁B₁C₁D₁, М - середина ребра D₁C₁, К и М одновременно являются серединами ребер PQ и BS правильного тетраэдра PQRS. D₁C₁ лежит на BS. Если ребро тетраэдра равно b, то \(|МК| = \frac{b\sqrt2}{2} = a\sqrt2\). Значит, b = 2a.

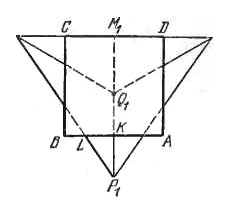
Спроектируем тетраэдр на плоскость ABCD (рис.), Р₁, Q₁, R₁, S₁ - проекции Р, Q, R, S. Поскольку PQ составляет с этой плоскостью угол 45°, то длина P₁Q₁ будет a√2.

Пусть L - точка пересечения прямой AB и прямой P₁R₁. Из подобия треугольников P₁LK и Р₁R₁М₁ найдем

$$ |LK|=\frac{|R_1M_1|\cdot|P_1K|}{|P_1M_1|}=\frac{a}{1+\sqrt2} \lt \frac{a}{2} $$

Значит, ребро тетраэдра PR (а, следовательно, и другие ребра: PS, QB и QS) пересекает куб.

Для вычисления объема получившегося тела удобно это тело рассматривать как тетраэдр со срезанными углами.

Ответ: \(\frac{a^3\sqrt2}{12}(16\sqrt2 - 17)\).