Основанием треугольной пирамиды ABCD является треугольник АВС, в котором ∠А = π/2, ∠С = π/6, |ВС| = 2√2. Длины ребер AD, BD и CD равны между собой. Сфера радиуса 1 касается ребер AD, BD, продолжения ребра CD за точку D и плоскости АВС. Найти величину отрезка касательной, проведенной из точки А к сфере.
Обозначим через К точку касания сферы с продолжением CD, а через М и L - точки касания с ребрами АD и BD, N - середина ВС (рис.).
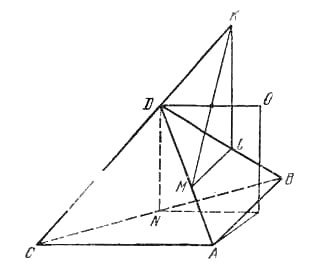
Так как |CD| = |DB| = |DA|, DN перпендикулярна плоскости ABC, |DK| = |DM| = |DL|, KL параллельна DN, ML параллельна АВ, значит, плоскость KLM перпендикулярна плоскости АВС, ∠KLM = 90°. Если O - центр сферы, то прямая DO перпендикулярна плоскости KLM, т. е. DO параллельна плоскости АВС, следовательно, |DN| = 1 (радиусу сферы). Кроме того, DO проходит через центр окружности, описанной около ΔKLМ, - середину КМ. Отсюда следует, что
$$ \angle{ODM} = \frac{1}{2}\angle{KDM} $$Далее,
$$ |DА| = |DC| = \sqrt{|CN|^2 +|DN|^2} = \sqrt3,\;\; |CA|=|CB|cos30° = \sqrt6, $$т. е. ΔCDA - прямоугольный, ∠CDA = 90°, ∠ODM = 45°, |DM| = |ОМ| = 1.
Искомый отрезок касательной равен |AM| = |AD| - |DM| = √3 - 1.
Похожие примеры: