Пусть О₁, O₂, O₃ - точки касания шаров с плоскостью Р, причем в точке O₁ касается шар радиуса r, а в O₂ и О₃ - радиусов R, О - вершина конуса (рис.), φ - угол между образующей конуса и плоскостью Р.

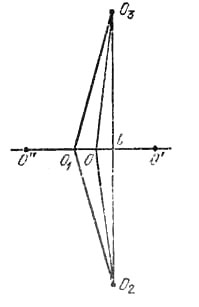
Можно найти, что

$$ |O_1O|=r ctg\frac{\phi}{2},\;\;|OO_2|=|OO_3|=R ctg\frac{\phi}{2},\\ |O_1O_2|=|O_1O_3|=2\sqrt{Rr},\;\;|O_2O_3|=2R $$

Поскольку |O₁O₂| = |O₁O₃|, то равным 150° может быть лишь угол ∠O₂O₁O₃, значит, R/r = 4 sin² 75° = 2 + √3

Далее, если L - середина О₂O₃, то

$$ |OL|=\sqrt{|OO_3|^2 - |O_3L|^2} = R\sqrt{ctg^2\frac{\phi}{2}-1},\\|O_1L|=\sqrt{|O_1O_3|^2 - |O_3L|^2} = \sqrt{4Rr - R^2} $$

Точка О находится на прямой О₁L, причем она может быть как на отрезке O₁L, так и на его продолжении за точки L или О, (на рисунке О’ и О’’). Соответственно получим три соотношения

$$ |O_1L|=|OO_1|+|OL|,\;\;|O_1L|=|O_1O’|-|O’L|,\;\;\\|O_1L|=|O’’L|-|O’’O_1| $$

Заменив в каждом из этих трех соотношений R = (2 + √3)r, \(ctg\frac{\phi}{2}=x\), в первых двух придем к противоречию:

$$ x=1\;\;\; \text{или} \;\;\; x= -\frac{2\sqrt3}{3}$$

в третьем же случае найдем \(x= \frac{2\sqrt3}{3}\)

Ответ: \(cos\phi = \frac{1}{7}\).