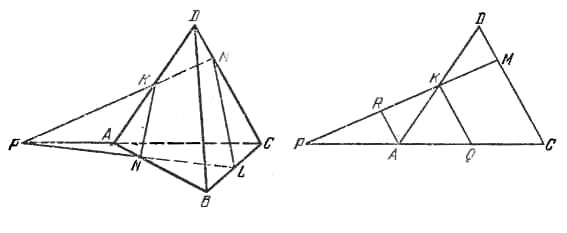
Обозначим через К и L середины ребер AD и ВС, N и Р - точки пересечения проведенной плоскости с прямыми AB и АС (рис.). Найдем отношения |РА|/|PC| и |РК|/|РМ|. Проведем KQ и AR параллельно DC, Q - середина АС.

$$ |AR|=|DM|,\;\;\frac{|PA|}{|PC|}=\frac{|AR|}{|MC|}=\frac{|DM|}{|MC|}=\frac{2}{3} \\\frac{|PK|}{|PM|}=\frac{|KQ|}{|MC|}=\frac{|DC|}{2|MC|}=\frac{5}{6} $$

Затем найдем

$$ \frac{|AN|}{|NB|}=\frac{2}{3},\;\;\frac{|PN|}{|PL|}=\frac{4}{5},\\ \frac{V_{PAKN}}{V_{ABCD}}=\frac{|PA|\cdot|AK|\cdot|AN|}{|AC|\cdot|AD|\cdot|AB|}=\frac{2}{5} $$

т.е. \(V_{PAKN}=2\). Поскольку высота, опущенная из A на PNK, равна 1, \(S_{PNK}=6\),

$$ \frac{S_{PML}}{S_{PNK}}=\frac{|PK|\cdot|PN|}{|PM|\cdot|PL|}=\frac{2}{3},\;\;S_{PML}=9 $$

Таким образом, площадь сечения будет:

$$ S_{PML} - S_{PNK} = 3 $$