Проведем сечение плоскостью, проходящей через ребро АВ и точку L - середину CD, К - точка пересечения плоскости Р и AL, высота, опущенная из А на BL, пересекает ВК в точке N, BL - в точке Q (рис.).

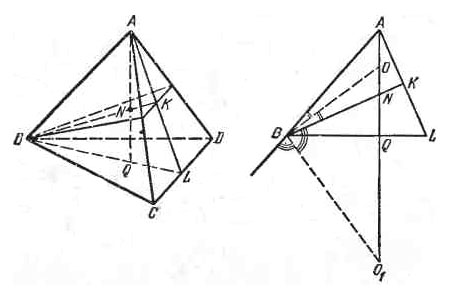
Нетрудно доказать, что центр сферы лежит на прямой AQ. При этом центр сферы может быть на отрезке AN (точка О) и на продолжении AQ (точка О₁).

Радиус первой сферы равен радиусу окружности, касающейся АВ и ВК и имеющей центр на AN. Обозначим его через x; x можно найти из соотношения:

$$ S_{BAN}=\frac{1}{2}(|AB|+|BN|)x, \\ |BN|=\frac{4}{5}|BK|=\frac{2}{5}\sqrt{2|AB|^2+2|BL|^2-|AL|^2}=\frac{\sqrt{11}}{5}a,\\ S_{BAN}= \frac{2}{5}S_{BAL}=\frac{\sqrt2}{10}a^2 $$

значит, \(х = \frac{\sqrt2a}{5+\sqrt{11}}\). Так же находится радиус второй сферы.

Ответ: \(\frac{\sqrt2a}{5\pm\sqrt{11}}\)