Если плоскость пересекает ребра AD и CD, то в сечении будет треугольник, при этом радиус вписанной окружности будет меняться от 0 до \(\frac{a}{\sqrt2(2cos\alpha +\sqrt{4cos^2\alpha+1})}\)

Пусть теперь плоскость пересекает ребра АВ и ВС в точках Р и N, SA и SC - в точках Q и В, SD - в точке К и продолжения AD и CD - в точках L и М (рис.).

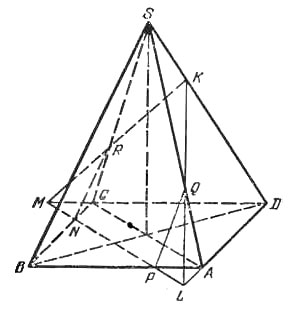
Поскольку прямые PQ и NB параллельны и касаются окружности, вписанной в наше сечение, то PN есть диаметр этой окружности. Обозначим |PN| = 2r, и получим следующее:

$$ |ML|=2a\sqrt2 - 2r, \\ |KL|=\frac{a\sqrt2-r}{2cos\alpha}\sqrt{4cos^2\alpha+1}, \\S_{MKL}=\frac{(a\sqrt2-r)^2}{2cos\alpha} $$

Таким образом,

$$ r=\frac{a\sqrt2 - r}{2cos\alpha + \sqrt{4cos^2\alpha+1}} $$

откуда

$$ r=\frac{a\sqrt2}{1+2cos\alpha + \sqrt{4cos^2\alpha+1}} $$

Ответ:

$$ 0\lt r\leq\frac{a}{\sqrt2(2cos\alpha + \sqrt{4cos^2\alpha+1})}, \\ r=\frac{a\sqrt2}{1+2cos\alpha + \sqrt{4cos^2\alpha+1}} $$