Точка О - общая вершина двух равных конусов, расположенных по одну сторону от плоскости α так, что только одна образующая каждого конуса (ОА для одного конуса и ОВ для другого) принадлежит плоскости α. Известно, что величина угла между высотами конусов равна β, а величина угла между высотой и образующей конуса равна φ, причем 2φ < β. Найти величину угла между образующей ОА и плоскостью основания другого конуса, которой принадлежит точка В.
Искомый угол дополняет до π/2 угол между образующей ОА и осью второго конуса. Обозначим через Р и Q центры оснований данных конусов, через S - точку, в которой плоскости оснований конусов пересекают перпендикуляр, восставленный к плоскости ОАВ в точке О (рис.).
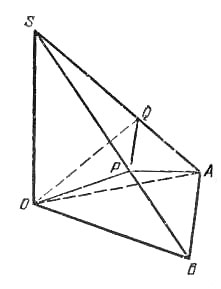
В пирамиде SOAB известно |ОА| = |ОВ|, SO перпендикулярно плоскости ОАВ, ОР и OQ перпендикулярны соответственно SB и SA, ∠РОB = ∠QOA = φ, ∠POQ = β. Надо найти ∠POA.
Пусть |ОА| = |ОВ| = l, |АВ| = a. Тогда
$$ |OP| = |OQ| = l cos\phi,\;\;|SA|=|SB|=\frac{l}{sin\phi},\\ |SP|=|SQ|=|OP|ctg\phi=l\frac{cos^2\phi}{sin\phi}, \\ |PQ|=|AB|\frac{|SP|}{|SB|}=a cos^2\phi $$С другой стороны,
$$ |PQ|=2|OP|sin\frac{\beta}{2}=2l cos\phi sin\frac{\beta}{2} $$Отсюда
$$ a cos\phi = 2l sin\frac{\beta}{2} \;\;\;\;\;\;\;\;\;\;\;(1)$$Найдем теперь |РА|:
$$ |PA|^2=|PB|^2 +|AB|^2 - 2|PB|\cdot|AB|cos{PBA}=\\=l^2sin^2\phi + a^@-2l sin\phi\cdot a\frac{asin\phi}{2l}=\\=l^2sin^2\phi+a^2cos^2\phi $$Но, если γ = ∠РОА, то из ΔРОА имеем:
$$ |PA|^2= l^2cos^2\phi +l^2 -2l^2 cos\phi cos\gamma $$Приравнивая два выражения для |РА|2 и учитывая (1), найдем
$$ cos\gamma = cos\phi - \frac{2sin^2\frac{\beta}{2}}{cos\phi} $$Ответ: \(\frac{\pi}{2} - arccos(cos\phi -\frac{2sin^2\frac{\beta}{2}}{cos\phi})\).
Похожие примеры: