В правильной призме ABCA1B1C1 длина бокового ребра и высота основания равна a. Через вершину А проведены две плоскости: одна перпендикулярно прямой АВ1, вторая перпендикулярно прямой АС1. Через вершину A1 также проведены две плоскости: одна перпендикулярно прямой А1В, вторая перпендикулярно прямой A1C. Найти объем многогранника, ограниченного этими четырьмя плоскостями и плоскостью BB1C1C.

Проведем через ребро АА1 плоскость, перпендикулярпую плоскости ВСС1B1 (рис.).

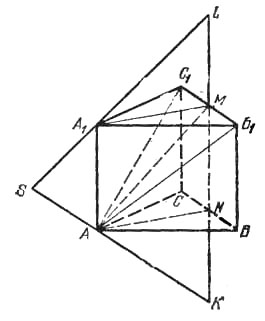
М и N - точки пересечения этой плоскости с С1В1 и СВ. Возьмем на MN точку К так, что |NК| = |MN|. По условию AA1MN - квадрат, значит, АК перпендикулярна AM, следовательно АК перпендикулярна плоскости АС1В1, т. е. АК есть прямая, по которой пересекаются плоскости, проходящие через вершину А.

Аналогично для вершины А1 определим точку L. Прямые АК и A1L пересекаются в точке S. Таким образом, наш многогранник представляет собой четырехугольную пирамиду SKPLQ с вершиной S, основание которой находится в плоскости ВВ1C1C. Далее, B1N есть проекция АВ1. Отсюда следует, что плоскость, проходящая через А перпендикулярно АВ1, пересекается с плоскостью ВВ1C1C по прямой, перпендикулярной B1N. Из условия следует, что ΔB1NC1 - правильный. Значит, четырехугольник PLQK, являющийся основанием пирамиды SPLQK, есть ромб, составленный из двух правильных треугольников со стороной |KL| = За.

Ответ: \(\frac{9a^3\sqrt3}{4}\)





Похожие примеры:
В параллелепипеде длины трех ребер, выходящих из общей вершины, равны соответственно а, b и с. Ребра а и b взаимно перпендикулярны, а ребро с образует с каждым из них угол α. Определить объем параллелепипеда, боковую поверхность его и угол между ребром с и плоскостью основания. (При каких значениях угла α задача возможна?) Смотреть решение→
В основании наклонной призмы лежит прямоугольный треугольник ABC с катетом ВС = а. Вершина В1верхнего основания проектируется на середину катета ВС. Двугранный угол, образованный боковыми гранями, проводящими через катет ВС и гипотенузу АВ, равен α. Боковые ребра наклонены к плоскости основания под углом β. Определить боковую поверхность призмы. Смотреть решение→
В основании прямой призмы ABCA1B1C1 лежит прямоугольный треугольник ABC с углом β при вершине В (β < 45°). Разность между площадями ее боковых граней, проходящих через катеты ВС и АС, равна S. Найти площадь сечения призмы плоскостью, образующей с плоскостью основания угол φ и проходящей через три точки: вершину В1 угла β верхнего основания, середину бокового ребра АА1 и точку D, расположенную на плоскости основания симметрично с вершиной В относительно катета АС. Смотреть решение→