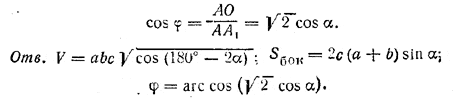В параллелепипеде длины трех ребер, выходящих из общей вершины, равны соответственно а, b и с. Ребра а и b взаимно перпендикулярны, а ребро с образует с каждым из них угол α. Определить объем параллелепипеда, боковую поверхность его и угол между ребром с и плоскостью основания. (При каких значениях угла α задача возможна?)

Проведем через вершину А₁ (рис.) плоскости A₁ЕО перпендикулярно к АВ и A₁FO перпендикулярно к AD.

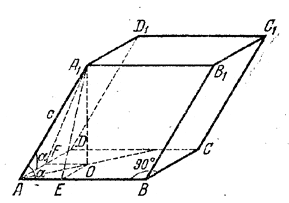
Эти плoскости будут перпендикулярны к плоскости основания (доказать!) и линия их пересечения A₁O будет высотой параллелепипеда. Образовавшиеся прямоугольные треугольники А₁АЕ и A₁AF равны между собой (по общей гипотенузе АА₁ = с и равным углам ∠ A₁AE = ∠ A₁AF = α). Следовательно, A₁E = A₁F и поэтому будут равны треугольники А₁ОЕ и A₁OF, а значит, OE = OF и прямая АО - биссектриса угла BAD.

Имеем H = √A₁E² - ОE². Так как AEOF - квадрат, то ОЕ=АЕ. Находим AE и А₁Е из треугольника AA₁E; получаем Н = с √sin² α - cos²α = с √1 - cos 2α.

Замечание. В трехгранном угле при вершине А два плоских угла равны каждый α и третий угол прямой; следовательно, сумма двух плоских углов 2α должна быть больше третьего (90°), т. е. 2α > 90° или α > 45°. При этом условии - cos2α > 0 и, следовательно, Н имеет действительное значение. Боковое ребро AA₁ образует с плоскостью основания ∠ A₁AО = φ, так как АО - проекция ребра на основание