Основанием пирамиды служит прямоугольный треугольник с гипотенузой, равной с, и острым углом α. Все боковые ребра наклонены к основанию под углом β. Найти объем пирамиды и плоские углы при вершине ее.
Высота пирамиды должна проходить через центр окружности, описанной около основания.
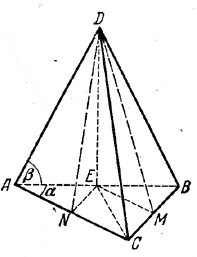
Но в прямоугольном треугольнике ABC (рис.) центр лежит на середине гипотенузы АВ в точке Е. Следовательно, AЕ, BE и СЕ будут проекциями боковых ребер AD, BD и CD на плоскость основания, так что ∠ DAE =∠ DBE = ∠ DCE = β. Объем пирамиды найдем по формуле
V = 1/3 • АС• СВ/2 • DE.
Из \(\Delta\)АВС имеем АС = с cos α , ВС = с sin α; из \(\Delta\)ADE находим DE = c/2tg β. Обозначим плоские углы при вершине: ∠ ADB = θ1 , ∠ BDC = θ2 и ∠ ADC = θ3. Так как эти треугольники равнобедренные, то высоты их DE, DM и DN пройдут через середины соответствующих сторон основания.
Из \(\Delta\)ABD ииеем ∠ θ1= 180°- β; из \(\Delta\)DBC имеем 
и из \(\Delta\)ADC имеем 
Из \(\Delta\)ADE находим 
и из \(\Delta\)АВС находим MB = ВC/2 = c/2 sin α и AN = AC/2 = c/2 cos α.
θ1= 180° - 2β,
θ2 =2 arcsin (sin α cos β),
θ3 = 2 arcsin (cos α cos β).