Основаниями правильной усеченной пирамиды служат квадраты со сторонами а и b (a > b). Боковые ребра наклонены к плоскости основания под углом α. Определить объем усеченной пирамиды и величину двугранных углов при сторонах оснований.
Усеченная пирамида изображается как в предыдущей задаче. Для изображения линейного угла искомого двугранного угла проводим А1Е и B1F (рис.) параллельно OO1 до пересечения с диагоналями АС и BD.
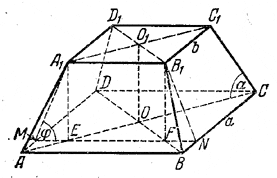
Проводим прямую EF; она будет параллельна АВ и пересечет ребра AD и ВС в точках М и N. Плоскость MA1B1N перпендикулярна к ребру AD, так как она проходит через прямые А1Е и MN, перпендикулярные к ребру. Следовательно, ∠ EMA1 = φ есть линейный угол двугранного угла при ребре AD.
Решение. Из трапеции MA1B1N получаем ![]()
Высоту усеченной пирамиды находим из треугольника АЕА1 , где
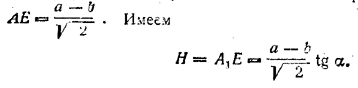
Объем находим по формуле V = H/3 (а2 + аb + b2). Искомый угол φ = ∠ EMA1 находим из треугольника A1ME, где ![]() (из трапеции MNB1A1). Имеем
(из трапеции MNB1A1). Имеем
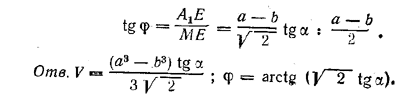
Похожие примеры: