Боковые ребра правильной усеченной треугольной пирамиды наклонены к плоскости основания под углом α. Сторона нижнего основания равна а, а верхнего — b (a > b). Найти объем усеченной пирамиды.

Сделав изображение правильной треугольной пирамиды DABC (рис.) , построим треугольник A₁B₁C₁, стороны которого соответственно параллельны сторонам треугольника ABC. Треугольник А₁В₁С₁ изображает верхнее основание усеченной пирамиды.

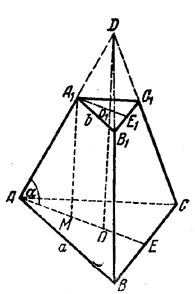
Изображение центра О₁ верхнего основания получается в пересечении DO с одной из медиан A₁E₁ треугольника А₁В₁С₁. Отрезок А₁М, параллельный ОО₁ и оканчивающийся в точке М, лежащей на медиане АЕ, изображает высоту усеченной пирамиды, опущенную из точки А₁ (отрезки DA₁, DB₁, DC₁ и DO₁ можно стереть).

Решение. Объем усеченной пирамиды

V= ^H/₃(Q + q + √Qq ),

где Q и q - площади треугольников ABC и А₁В₁С₁ , так что

Q =^√3/₄ а²; q = ^√3/₄b².

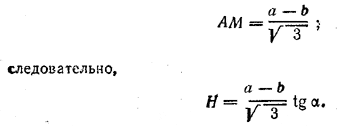
Высоту Н = А₁М найдем из треугольника АА₁М, где ∠ МАА₁ = α и АМ = АО - А₁O₁. Но АО и А₁O₁ - это радиусы окружностей, описанных около ABC и А₁В₁С₁ Поэтому, АО = ^a/_√3 и А₁O₁ = ^b/_√3 Значит,

Ответ: V = ¹/₁₂ (а³ - b³) tg α.