В треугольной пирамиде две боковые грани суть равнобедренные прямоугольные треугольники, гипотенузы которых равны b и образуют между собой угол α. Определить объем пирамиды.

Все боковые ребра пирамиды равны как стороны равнобедренных прямоугольных треугольников, поэтому высота DO пирамиды будет проходить через центр О окружности, описанной около основания;

S_ocн. = ¹/₂ b² sin α

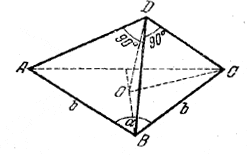
Из треугольника DOC находим

Н = √DC²- ОС² ,

где DC = ^b/_√2 , а OC = R есть радиус окружности, описанной около треугольника ABC. Так как треугольник ABC - равнобедренный, то ∠ BAC = 90° - ^α/₂ и, следовательно, по теореме синусов

ВС = 2R sin (90° - ^α/₂),

откуда

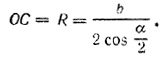
Ответ: V = ¹/₆ b² sin ^α/₂ √cos α