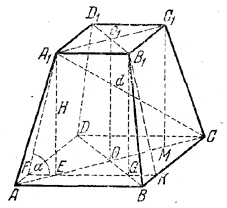
В правильной усеченной четырехугольной пирамиде даны: диагональ d, двугранный угол αпри нижнем основании и высота H. Найти объем усеченной пирамиды.

Из треугольника A₁FE (рис.), где ∠ A₁FE = α, находим FE = H ctg α, a из треугольника А₁СЕ, где A₁C = d, находим EC = √d² - H² и, следовательно,

Теперь находим стороны оснований

AB = a = EK + EF

и

A₁B₁ = EG = b = EK- GK = EK- EF,

так что для величины

a²+ ab + b²,

входящей в формулу объема усеченной пирамиды, получаем выражение

(EK+ EF)²+ (EK+EF) (EK-EF) + (EK-EF)² = 3EK²+EF²

Ответ: V = ^H/₃(3 • ЕК² + EF²) = ^H/₆[ 3 (d² - H²) + 2H² ctg² α].