Боковое ребро правильной четырехугольной усеченной пирамиды равно l, оно наклонено к плоскости основания под углом β. Диагональ пирамиды перпендикулярна к боковому ребру ее. Определить объем пирамиды.

Можно использовать тот же рис., что и в предыдущей задаче, введя обозначения AA₁ = l и ∠ А₁АС = β.

Из прямоугольною треугольника AA₁C находим так что

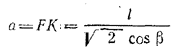
Из треугольника AA₁E находим H = l sin β и AE = l cos β так что

следовательно,

Теперь получим

Если числитель и знаменатель помножить на (1+cos 2β) (применив формулу для суммы кубов), то получим несколько более простое выражение.

Замечание. Угол β должен быть больше 45", так как FK > 2•FE. Поэтому cos 2β < 0.