В прямоугольном треугольнике гипотенуза с, а один из острых углов равен α. Определить радиус вписанного круга.

Так как АО (рис.) есть биссектриса угла α = ∠CAD, то ∠BAO = ^α/₂ .

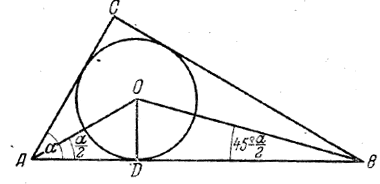
Таким же образом получаем ∠ABO = ¹/₂(90°- α) = 45°- ^α/₂. Из треугольников AOD и BOD имеем

AD = OD ctg ^α/₂ и DB = OD • ctg (45° - ^α/₂).

Следовательно,

с = АВ = AD + DB = OD [ctg ^α/₂+ ctg (45° - ^α/₂)]

Отсюда находим

.

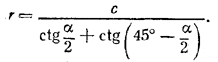Знаменатель можно преобразовать к виду, удобному для логарифмирования:

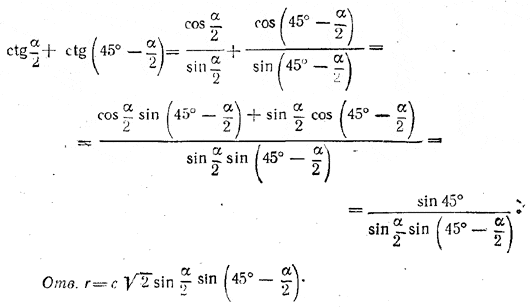
Замечание. Применив формулу r = S : p (S - площадь треугольника, р - полупериметр), мы получили бы решение в равносильном виде