В прямоугольном треугольнике найти отношение катетов, если высота и медиана, выходящие из вершины прямого угла, относятся, как 40 : 41.

По условию BD : BE = 40 : 41 (рис.).

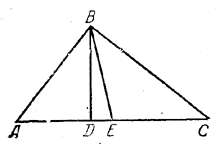
Примем за единицу длины 1/40 часть BD. Тогда BD = 40, BE = 41. Так как треугольник ABC прямоугольный и BE - медиана прямого угла, то АЕ = ВЕ = 41. Треугольник BDE прямоугольный, поэтому

BЕ = √BЕ2- BD2 = 9.

Следовательно, AD = AE - DE = 32. Из подобия треугольников ABD и ABC находим

АB/ВC = АD/ВD = 32/40 = 4/5

Ответ: АB/ВC = 4/5





Похожие примеры:
Основанием пирамиды является прямоугольный треугольник с катетами 6 и 8. Вершина пирамиды удалена от плоскости ее основания на расстояние, равное 24, и проектируется на эту плоскость в точку, лежащую внутри основания. Найти ребро куба, четыре вершины которого лежат в плоскости основания данной пирамиды, а ребра, соединяющие эти вершины, параллельны соответствующим катетам треугольника, лежащего в основании пирамиды. Четыре другие вершины куба лежат на боковых гранях данной пирамиды. Смотреть решение→
В основании наклонной призмы лежит прямоугольный треугольник ABC, сумма катетов которого равна m и угол при вершине А равен α. Боковая грань призмы, проходящая через катет АС, наклонена к основанию под углом β. Через гипотенузу AВ и через вершину С1 противоположного трехгранного угла проведена плоскость. Определить объём отсеченной треугольной пирамиды, если известно, что боковые ребра ее равны между собой. Смотреть решение→
Дана треугольная призма AВСА1В1С1. Известно, что пирамиды ABCC1, АВВ1С1 и АА1В1С1 равны между собой. Найти двугранные углы между плоскостью основания и боковыми гранями призмы, если в основании лежит неравнобедренный прямоугольный треугольник. Смотреть решение→