Основанием пирамиды является прямоугольный треугольник с катетами 6 и 8. Вершина пирамиды удалена от плоскости ее основания на расстояние, равное 24, и проектируется на эту плоскость в точку, лежащую внутри основания. Найти ребро куба, четыре вершины которого лежат в плоскости основания данной пирамиды, а ребра, соединяющие эти вершины, параллельны соответствующим катетам треугольника, лежащего в основании пирамиды. Четыре другие вершины куба лежат на боковых гранях данной пирамиды.

Сначала изобразим то сечение A₁M₁B₁ (рис.), где лежит «верхняя» грань куба K₁L₁M₁N₁ (это сечение есть прямоугольный треугольник с прямым углом при вершине M₁). Так как вершины К₁L₁М₁N₁ лежат на боковых гранях, то они находятся на сторонах треугольника A₁M₁B₁ (М₁ совпадает с вершиной прямого угла, прямая M₁K₁ изображает биссектрису прямого угла, ибо M₁N₁= M₁L₁). Теперь изображаем куб KLMNK₁L₁M₁N₁. Внутри четырехугольника K₁L₁M₁N₁берем произвольную точку О₁, изображающую пересечение высоты DO с гранью K₁L₁M₁N₁ и соединяем ее с точкой О, сходственно расположенной в четырехугольнике KLMN. Проводим прямые O₁A₁, O₁В₁ , O₁M₁ и прямые ОА, ОВ, ОМ, соответственно им параллельные. В пересечении DA₁, DB₁ и DM₁ соответственно с ОА, ОВ и ОМ находим точки А, В, С - вершины основания пирамиды.

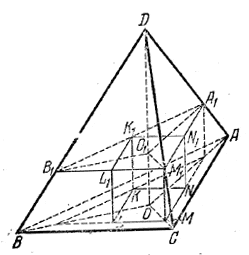
Решение. По условию AС = 6; ВС = 8; DO = 24 (На рис. эти соотношения не соблюдены.).

Обозначим ребро куба через х. Тогда OO₁ = х и DO₁ = 24 - х. По свойству сечений, параллельных основанию пирамиды, имеем В₁М₁ : ВС = DO₁ : DO, т. е. В₁M₁ : 8=
= (24 - х) : 24, откуда

Из подобия треугольников K₁B₁L₁ и ABC имеем

K₁L₁ : B₁L₁= 6 : 8;

здесь

Следовательно, , откуда x = 3.

Ответ: 3.