В правильную четырехугольную пирамиду вписан куб так, что вершины его лежат на апофемах пирамиды. Найти отношение объема пирамиды к объему куба, зная, что угол между высотой пирамиды и ее боковой гранью равен α.
Из треугольника EOF (рис.), где OF = a/2 и ∠ OEF = α, имеем Н = a/2 ctg α.
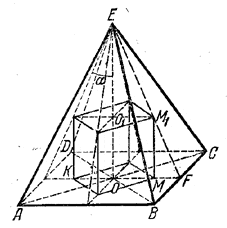
Следовательно, объем пирамиды
V = 1/3 а2H = 1/6 a3 ctg α.
Выразим сторону а через ребро куба x = MM1. Имеем
а = 2 OF = 2ОМ +2MF = KM + 2MM1 • tg α = х√2 + 2х tg α.
Следовательно,
![]()
Здесь х3=V1, есть объем куба.
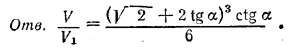
Похожие примеры: