Основанием пирамиды служит равнобедренный треугольник ABC, где АВ=АС. Высота пирамиды SO проходит через середину высоты AD основания. Через сторону ВС проведена плоскость перпендикулярно к боковому ребру AS, образующая с основанием угол α. Определить объем пирамиды, отсеченной от данной и имеющей с ней общую вершину S, если объем другой отсеченной части ее равен V.
Через прямую линию можно продести плоскость, перпeндикулярную к другой прямой, только в том случае, если эти прямые перпендикулярны.
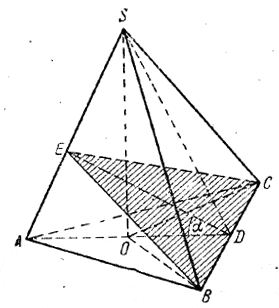
Докажем, что BC⊥AS (рис.). Проведем плоскость ASO через ребро AS и высоту SO. Так как А и О принадлежат плоскости ASO и nbsp; одновременно плоскости основания ABC, то эти плоскости пересекутся по прямой АО, т. е. по высоте AD равнобедренного треугольника ABC. Треугольники OCD и OBD равны (доказать!), поэтому ОВ = ОС; следовательно, наклонные SC и SB тоже равны, а значит, прямая SD, являющаяся медианой равнобедренного треугольника BSC, служит и его высотой. Так как прямые AD и SD, по доказанному, перпендикулярны к ребру ВС, то ребро ВС перпендикулярно к плоскости ADS, a значит, и к прямой AS, лежащей в этой плоскости, что и требовалось доказать.
Чтобы провести через ВС плоскость, перпендикулярную к AS, достаточно опустить перпендикуляр DE на прямую AS. Плоскость ВЕС перпендикулярна к ребру AS, так как две прямые, лежащие на ней (DE и ВС), перпендикулярны к AS.
Плоскость ADS, перпендикулярная к ребру ВС, в пересечении с двугранным углом α дает угол ADE (линейный угол этого двугранного угла).
Треугольник ASD - равнобедренный (так как высота SO проходит через середину основания AD). Следовательно,
∠ ASD = 2 ∠ ASO = 2α
(∠ ASO = ∠ ADE = α как углы с перпендикулярными сторонами). Отношение объема V; пирамиды SBCE к объему V пирамиды АВСЕ (эти пирамиды имеют общее основание ВСЕ) равно отношению высот, т. е. V1 : V= SE : AE. Из треугольника DSE имеем
SE = DE • ctg ∠ ESD = DE • ctg 2α;
из треугольника AED находим
AE = DE • tg α;.
Следовательно,
V1 : V= ctg2α : tg α.
Ответ: V1 = V ctg α ctg 2α.