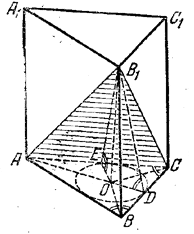
В основании призмы АВСА1В1С1 лежит равнобедренный треугольник ABC (AB=AC и ∠ABC = α). Вершина В1верхнего основания призмы проектируется в центр окружности радиуса r, вписанной в нижнее основание. Через сторону АС основания и вершину В1 проведена плоскость, наклоненная к плоскости основания под углом α. Найти полную поверхность отсеченной треугольной пирамиды АВСВ1 и объем призмы.
Плоскость отсекает от призмы пирамиду B1ABC (рис.), высота которой проходит через центр О окружности, вписанной в основание пирамиды; поэтому все боковые грани ее образуют с плоскостью основания равные углы α ;
следовательно,
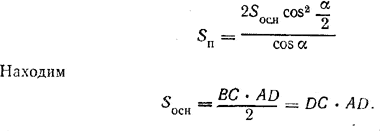
(См. задачу 425)
Из \(\Delta\)OCD, где OD = r и ∠ OCD = α/2, находим DC = r ctg α/2.
Из \(\Delta\)ADC находим AD = DC • tg α = r ctg α/2 tg α.
Следовательно,
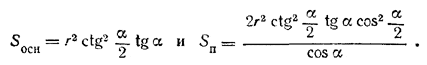
Полученные выражения можно упростить, представив tg α в виде
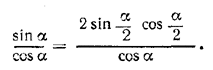
Объем призмы
V = Socн. • H ,
где H = r tg α (из \(\Delta\)B1OD).
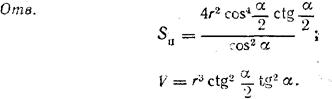
Похожие примеры: