Основанием пирамиды служит прямоугольный треугольник, а высота ее проходит через точку пересечения гипотенузы с биссектрисой прямого угла основания. Боковое ребро, проходящее через вершину прямого угла, наклонено к плоскости основания под углом α. Определить объем пирамиды и углы наклона боковых граней к плоскости основания, если биссектриса прямого угла основания равна m и образует с гипотенузой угол 45° + α.
Из \(\Delta\)ВМС (рис.),
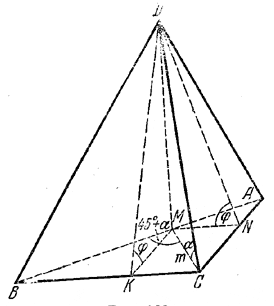
где ∠MCВ = 45°, а ∠МВС = 180°- (45°+ α ) - 45° = 90°- α , по теореме синусов имеем
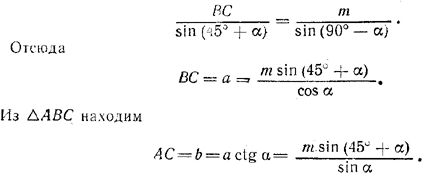
Из \(\Delta\)DCM находим H = m tg α.
Линейными углами для двугранных DACB и DBCA будут ∠DNM и ∠DKM; эти углы равны, так как равны треугольники MКС и MNC (по гипотенузе и острому углу) и треугольники DMK и DNM (по гипотенузе и катету). Обозначим их величину через φ;
тогда tg φ = H/MN , где MN = m/√2
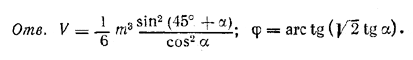
Похожие примеры: