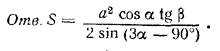Основанием пирамиды является равнобедренный треугольник с боковой стороной аи углом αпри основании (α > 45°). Боковые ребра наклонены к плоскости основания под углом β. В этой пирамиде проведена плоскость через ее высоту и вершину одного из углов α. Найти площадь сечения.
На рис. OA= OC = R- радиусы окружности, описанной «коло равнобедренного треугольника ABC (АВ = АС = а).
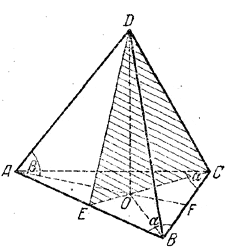
В силу условия α > 45° центр О лежит внутри треугольника AВС (при α < 45° угол ,4 = 180° - 2α был бы тупым, центр описанной окружности лежал бы вне треугольника ABC, и тогда плоскость, проведенная через высоту пирамиды и вершину С, не дала бы никакого сечения пирамиды). Высота пирамиды проходит через центр О (см. задачу 419 ).
Из треугольника AOD имеем H = R tg β. Так как по теореме синусов AC = a = 2R sin α, то ![]()
Найдем теперь основание СЕ сечения из треугольника АСЕ. В нем ∠ CAE = 180° - 2α, a ∠ ACE, лежащий в основании равнобедренного треугольника АОС (АО = ОС = R), равен ∠ CAO = 1/2 ∠ CAE = 90° - α. Значит, ∠AEC = 3a - 90°. По теореме синусов
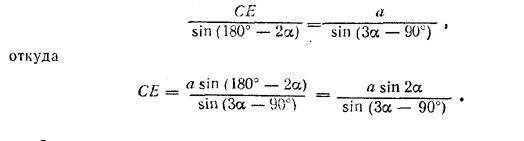
Замечание. В знаменателе можно написать (-cos 3α); но угол 3α заключен между 135° и 270°, так как 45° < α < 90°; таким образом, (-cos 3α) есть положительное число. Поэтому при вычислениях с таблицами удобнее иметь дело с углом 3α-90°, заключенным между 45° и 180°.