Основанием правильной пирамиды служит многоугольник, сумма внутренних углов которого 540°. Определить объем этой пирамиды, зная, что боковое ребро ее, равное l, наклонено к плоскости основания под углом α.

Основание пирамиды есть правильный пятиугольник (из уравнения 180°(n - 2) =540° находим п = 5).

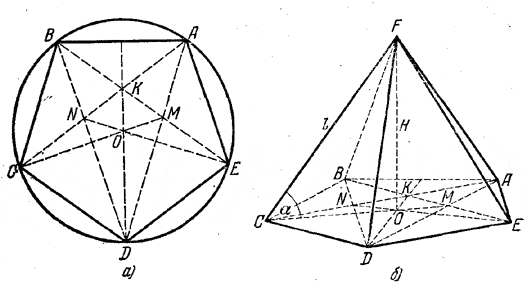
А в правильном пятиугольнике ABCDE (рис., а) каждая диагональ (например AD) делится каждой другой (например BE) в крайнем и среднем отношении, так что

Кроме того, каждая диагональ параллельна одной из сторон (например AD || BC). Центр О лежит на пересечении СМ и EN. Поэтому изображение правильного пятиугольника можно построить следующим образом.

Строим произвольный треугольник ABD (рис., б). Делим стороны AD и BD точками М и N в крайнем и среднем отношении - приблизительно в отношении

AM : MD = 2 : 3;

достаточно разделить одну сторону и провести MN || AB. Проводим AE || BD до пересечения с продолжением прямой ВМ в точке Е. Аналогично строится точка С. Изображение центра О лежит в пересечении СМ и EN.

Решение. Из треугольника COF, в котором ∠OCF = α и CF = l, находим
H = OF = l sin α; OC = l cos α. Площадь основания

S = 5• ¹/₂•ОС•OD•sin ∠COD = ⁵/₂•ОС²•sin 72° = ⁵/₂l² cos² α sin 72°

Ответ: V = ¹/₃ SH = ⁵/₆ l³ sin 72° cos² α sin α.