Определить углы, составляемые с основанием боковым ребром и боковой гранью правильной пятиугольной пирамиды, у которой боковые грани — равносторонние треугольники.

Об изображении правильного пятиугольника см. в предыдущей задаче.

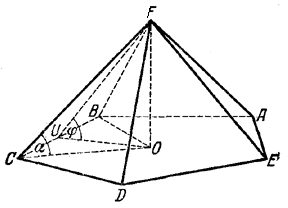
Для определения угла α рассмотрим треугольник COF (рис.), где FC = CB= a (по условию треугольник CBF равносторонний). Сторона же ОС (радиус описанного круга) выражается через а из треугольника COU, где угол COU равен 36° и CV = a/2

Имеем так что

Угол φ определяется из треугольника OUF, где FU = a√3/2 (как высота равностороннего треугольника со стороной a), a из треугольника COU).

Имеем





Похожие примеры:
Доказать, что середины сторон треугольника, основания высот и середины отрезков высот, заключенных между каждой из вершин и точкой пересечения высот, представляют собой девять точек, лежащих на одной окружности. Показать, что центр этой окружности лежит на середине отрезка, соединяющего точку пересечения высот данного треугольника с центром описанного круга, а радиус равен половине радиуса описанного круга.  Смотреть решение→
Пусть длины а, b, с сторон треугольника удовлетворяют неравенствам а < b < с, образуя арифметическую прогрессию. Доказать, что ac = 6Rr, где R — радиус описанного, а r — радиус вписанного в треугольник круга.  Смотреть решение→
Доказать, что в любом треугольнике радиус описанного круга R и радиус вписанного круга r связаны с расстоянием l между центрами этих кругов соотношением

l 2 = R2 — 2Rr  Смотреть решение→