Доказать, что в любом треугольнике радиус описанного круга R и радиус вписанного круга r связаны с расстоянием l между центрами этих кругов соотношением

l ² = R² — 2Rr

Пусть К и О — центры описанного и вписанного в \(\Delta\)AВС кругов и D — середина дуги АС.

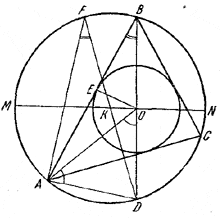
Каждый из углов, ∠ОАD и ∠AOD, равен половине суммы углов при вершинах А и В треугольника ABC. Отсюда следует, что OD = AD.

По теореме о хордах, пересекающихся внутри круга, имеем

MO • ON = BO • OD.

Далее, если ОЕ ⊥ АВ и FD - диаметр, то треугольники ВОЕ и FDA подобны, откуда ВО : ОЕ = FD : AD, так что BO • AD = OE • FD или, так как AD = OD, BO • OD = OE • FD. Следовательно,

MO • ON = OE • FD.

Подставив в это равенство значения МО = R + l, ON = R — l, OE = r, FD = 2R, получим R² — l² = 2Rr, что и требовалось доказать.