На сторонах треугольника ABC взяты точки Р, Q, R так, что три прямые АР, BQ и CR пересекаются в одной точке. Доказать, что

AR•BP•CQ = RB•PC•QA.

Прямые АР, BQ и CR разбивают треугольник ABC на шесть треугольников:
\(\Delta\)AOR, \(\Delta\)ROB, \(\Delta\)ВОР, \(\Delta\)РОС, \(\Delta\)COQ, \(\Delta\)QOA.

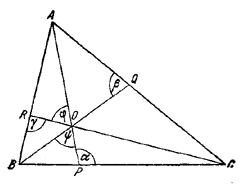
Применяя теорему синусов к каждому из них, получаем:

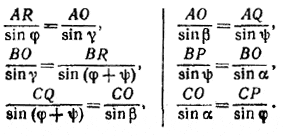
Перемножив почленно все эти равенства, находим: AR•BP•CQ = BR•AQ•CP.