Внутри правильного треугольника ABC взята произвольная точка Р, из которой опущены перпендикуляры PD, РЕ и PF соответственно на ВС, СА и АВ. Вычислить \(\frac{PD + PE + PF}{BD + CE + AF} \)
Проведем через точку Р три прямые, параллельные сторонам треугольника (рис.).
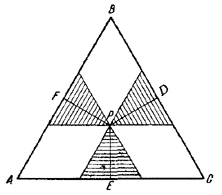
Три образовавшихся треугольника (заштрихованные на рисунке) также правильные, и сумма их сторон равна стороне АВ = а треугольника ABC.
Значит и сумма их высот равна высоте \(\Delta\)ABC, так что
![]()
Сумма BD + CE + AF равна сумме сторон заштрихованных треугольников, сложенной с суммой половин этих же сторон, так что:
BD + CE + AF = 3/2а.
Следовательно,
\( \frac{PD + PE + PF}{BD + CE + AF} = \frac{1}{\sqrt3} \)
Похожие примеры: