Пусть пятиугольник ABCDE является проекцией правильного пятиугольника, причем |АВ| = 1, |ВС| = 2, |CD| = a, ABCD - трапеция, в которой \(\frac{|AD|}{|BC|}=\lambda=\frac{1+\sqrt5}{2}\), F - точка пересечения ее диагоналей, AFDE - параллелограмм.

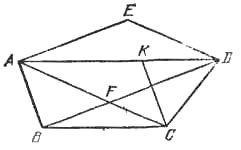
Проведем СК параллельно АВ. В ΔСKD имеем |СК| = 1, |KD| = 2(λ - 1), |CD| = a. Обозначим ∠CDК = φ. Запишем теорему косинусов для треугольников CKD и ACD:

$$ 1 = a^2+4(\lambda - 1)^2 - 4(\lambda - 1)a cos\phi, \\ |AC|^2 = a^2+4\lambda^2 -4a\lambda cos\phi $$

Из этих двух соотношений найдем

$$ |AC|=\sqrt{\frac{4\lambda^2 -3\lambda -a^2}{\lambda -1}}, \\ |ED|=|AF|=\frac{\lambda}{\lambda+1}\sqrt{\frac{4\lambda^2 -3\lambda -a^2}{\lambda -1}} $$

Аналогично находим

$$ |AE|=|FD|=\frac{\lambda}{\lambda+1}\sqrt{\frac{a^2\lambda - 1 + 4\lambda^2 -4\lambda}{\lambda -1}} $$

Ответ. Две другие стороны равны:

$$ \frac{\sqrt5 - 1}{4}\sqrt{14+10\sqrt5 - 2(\sqrt5+1)a^2}\;\; \text{и}\\ \frac{\sqrt5 - 1}{4}\sqrt{a^2(6+2\sqrt5) + 6(\sqrt5+1)} $$

Задача имеет решение при \(\sqrt5-2 \lt a \lt \sqrt5\).