В треугольнике ABC через точку пересечения биссектрис углов В и С проведена параллельно ВС прямая MN до пересечения в точках М и N соответственно со сторонами АВ и АС. Найти зависимость между отрезками MN, ВМ, CN.
Разобрать случаи:

1. обе биссектрисы внутренние;
2. обе биссектрисы внешние;
3. одна из биссектрис внутренняя, другая внешняя.

Когда М и N совпадут?

1) Пусть ВО и СО — биссектрисы внутренних углов \(\Delta\)ABC (рис.).

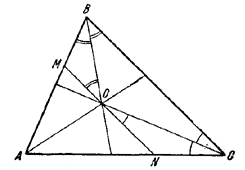
Легко видеть, что треугольники ВОМ и CON равнобедренные.

Следовательно, MN= BM + CN.

2) Зависимость MN = BM + CN имеет место и в случае внешних биссектрис.

3) Если одна из биссектрис внутренняя, а другая — внешняя (рис.), то из внутренних треугольников ВМО и CNO находим MN = CN — BM, когда CN > ВМ,
и MN = BM— СN, когда CN < ВМ.

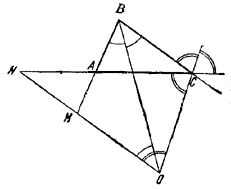
Итак, в этом случае

MN = |CN — BM|.

Точки М и N совпадают только в случае (3), если \(\Delta\)ABC равнобедренный (АВ = АС).