Если каждую из двух противолежащих сторон четырехугольника разделить на отрезки, пропорциональные прилежащим сторонам, то прямая соединяющая точки деления пересекает продолжения двух других сторон под равными углами
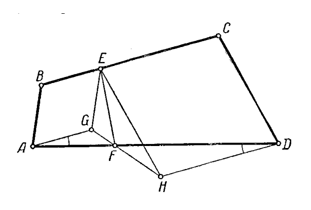
Пусть в четырехугольнике ABCD точка Е лежит на стороне ВС, а F – на стороне DA, причем ВЕ:ЕС = AF:FD = АВ:ВС.
Проведем через точки А, Е и D прямые, параллельные ВС, ВА, CD и СЕ, которые пересекаются в точках G и Н и образуют два параллелограмма – ABEG и ECDH.
Соединим точку F прямыми с G и Н. Тогда в треугольниках AGF и FDH AG:HD = ВЕ:ЕС = AF:FD и ∠GAF = ∠FDH, как накрест лежащие углы; следовательно, треугольники AGF и FDH подобны, откуда ∠AFG = ∠DFH и линия GFH – прямая.
Из подобия следует также, что AF:FD = GF:FH, и, следовательно, GH:FH = АВ:CD = GE:EH, т. е. прямая EF - биссектриса угла GEH и ∠GEF = ∠FEH, а это доказывает теорему.
Похожие примеры: