Доказать, что если через точки пересечения двух окружностей провести две параллельные прямые, то наибольшие отрезки этих прямых, ограниченные окружностями, равны

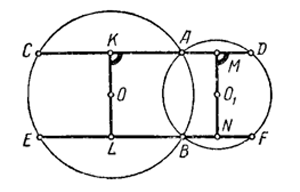
Пусть CD и EF – параллельные секущие, проходящие через общие точки окружностей А и В; CD и EF – отрезки, ограниченные окружностями.

Через О и О₁ проведем две прямые KL и MN перпендикулярно CD и EF. Тогда СК = КА, АМ = MD, EL = LB, BN = NF. Но KMNL – прямоугольник, а потому КМ = LN; а КМ и LN есть суммы половин хорд, следовательно, CD = EF.