Прямая пересекает параллельные стороны квадрата; вторая прямая, перпендикулярная первой, пересекает две другие стороны квадрата. Доказать, что отрезки этих прямых, ограниченные точками пересечения со сторонами квадрата, равны между собой.

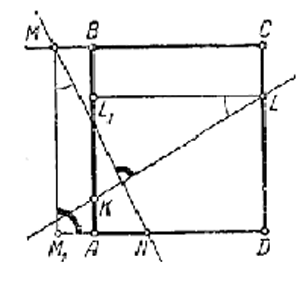
Пусть KL и MN – отрезки перпендикулярных прямых, заключенные между сторонами квадрата.

Проведем LL₁ ⊥ АВ, ММ₁ ⊥ AD.

В прямоугольных треугольниках KLL₁ и NMM₁ катеты LL₁ и MM₁ равны, так как каждый из них равен стороне квадрата;

∠KLL₁ = ∠NMM₁, как острые углы с взаимно перпендикулярными сторонами, а потому треугольники KLL₁ и NMM₁ равны, и, следовательно, KL = NM.