Внутри треугольника АВС взята точка М и построены параллелограммы АМВМ₁, ВМСВ₂, СМАМ₃. Доказать, что прямые АМ₂, ВМ₃, СМ₁ пересекаются в одной точке.

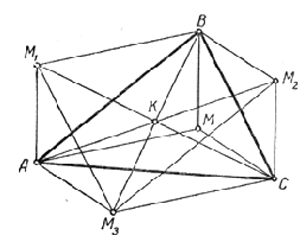
В параллелограмме МВМ₂С сторона ВМ₂ равна и параллельна стороне МС;
в параллелограмме МСМ₃А сторона АМ₃ равна и параллельна стороне МС, а потому равна ВМ₂ в четырехугольнике АВМ₂М₃ равна и параллельна стороне АМ₃, и, следовательно, АВМ₂М₃ – параллелограмм, а потому его диагонали АМ₂ и ВМ₃ в точке пересечения К делятся пополам.

Аналогично доказывается, что в параллелограмме СМ₃М₁В диагональ СМ₁ пересечет диагональ ВМ₃ в ее середине К; следовательно, прямые АМ₂, ВМ₃, СМ₁ пересекаются в одной точке.