Дан параллелограмм, в котором острый угол 60°. Определить отношение длин сторон, если отношение квадратов длин диагоналей параллелограмма равно ¹⁹/₇.

На рисунке, где ∠А = 60°, имеем

BD² = AD² + AB² - 2 • BA • AD • cos60° = a² + b² - ab,

AC² = a² + b² + ab.

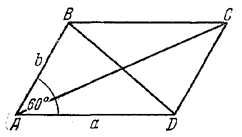
Так как АС больше BD, то данное отношение ¹⁹/₇ равно AC²/BD² (а не BD²/AC²)
Из уравнения

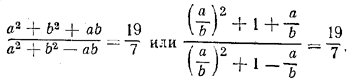
находим ^a/_b = ³/₂ и ^a/_b = ²/₃. Оба эти значения дают один и тот же параллелограмм (на рисунке можно изменить обозначения - обoзначить АВ через а и AD - через b).

Отв. Стороны относятся как 3 : 2.