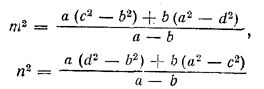По основаниям а и b и боковым сторонам с и d трапеции определить ее диагонали m и n.

При обозначениях рисунка имеем из треугольника ABC:

m² = b² + с² - 2bс cos B

а так как cos B = cos(180° - A) = - cos A, то т²= b² + с² + 2bс cos A. Из треугольника ADC находим

т²= a² + d² + 2ad cos D.

Приравнивая это выражение предыдущему, получаем

2bс cos A +2ad cos D = a²- b² + d²-с². (1)

Таким же образом, рассматривая треугольники ABD и CBD, получим

2ас cos A + 2bd cos D = a²- b²- (d²-с²). (2)

Из уравнений (1) и (2) можно найти cos А и cos D, а после этого найдем m² и n². Вычисление удобно вести так: помножим (1) на b, а (2) на а, после чего вычтем первое уравнение из второго. Получим

2(a² - b² )с cos A= (a² - b² ) (a - b) - (d² - с²) (a + b).

Разделив обе части равенства на (a² - b²) [\(\ne0\)], получим

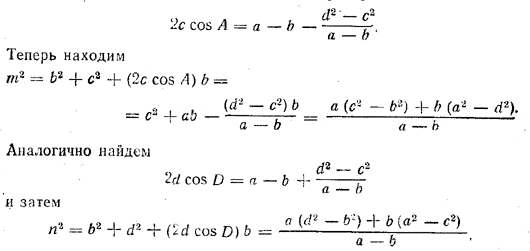
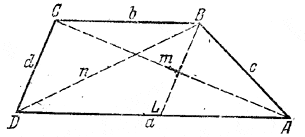
Замечание. Отрезок AD = a меньше ломаной ABCD. Поэтому задача может иметь решение лишь при условии a < b + c + d. Однако одного этого условия мало, что видно из следующего. Пусть а > b и c > d (если эти неравенства не выполняются, то всегда можно изменить обозначения и после этого неравенства будут иметь место).

Проведем прямую BL параллельно стороне CD. Получим параллелограмм DCBL, так что BL = CD = d и DL = CB = b. В треугольнике ALB сторона LA = DA - DL = a - b больше, чем разность сторон АВ = с и BL = d. Поэтому должно соблюдаться еще второе условие а - b > c - d. Если хотя бы одно из двух условий не выполнено, то по крайней мере одно из выражений, полученных для m² и n², окажется отрицательным.

Двух условий a < b + c + d и а - b > c - d уже достаточно, чтобы задача имела решение. Действительно, первое условие можно записать в виде а - b < c + d. Следовательно, можно построить треугольник ABL со сторонами AL = a - b, AB = c и BL = d. Продолжив сторону AL на расстояние LD = b и построив параллелограмм DLBC, получим четырехугольник ABCD; он будет трапецией с основаниями AD = a, BC = b и боковыми сторонами АВ = с и DC = d.

Отв.