В правильной четырехугольной призме проведены два параллельных сечения: одно проходит через середины двух смежных сторон основания и середину оси, другое делит ось в отношении 1:3. Зная, что площадь первого сечения равна S, найти площадь второго

Пусть NQN₁Q₁ и LML₂M₂ - параллельные сечения призмы, а - длина диагонали АС основания, H - длина отрезка KK₁.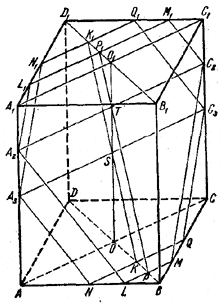

Тогда площадь первого сечения равна

S = ^H/₂ (a + ^a/₂) = ³/₄Ha

Площадь второго сечения будет

S' = ¹/₂ PT (A₂C₂ + LM) + ¹/₂ P₁T(A₂C₂ + L₁M₁).

Но

A₂C₂ = a, LM = ^a/₄ , L₁M₁= ³/₄а, РТ= ³/₄Н, P₁T = ¹/₄H,

что легко усматривается из подобия соответствующих треугольников. В силу этого получаем:

S' = ¹¹/₁₆ aH

и, следовательно,

S' = ¹¹/₁₂ S

Замечание. Эта задача может быть весьма просто решена другим путем, если принять во внимание формулу

S_пр. = S cosφ, (1)

где S - площадь некоторого многоугольника, расположенного в плоскости Р, S_пр. - площадь проекции этого многоугольника на плоскость Q, φ - угол между плоскостями Р и Q.

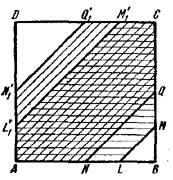
Согласно формуле (1) площади рассматриваемых в задаче параллельных сечений относятся как площади их проекций. И наша задача сводится к нахождению площадей двух фигур: L'₁M'₁CMLA и N'₁Q'₁CQNA (буквы со штрихами обозначают проекции соответствующих точек на основание призмы).