Треугольная пирамида рассечена плоскостью на два многогранника. Найти отношение объемов этих многогранников, если известно, что секущая плоскость делит три боковые ребра, сходящиеся в одной вершине пирамиды, в отношении 1:2, 1:2 и 2:1, считая от вершины.

Рассмотрим пирамиду KAEF, являющуюся одним из многогранников.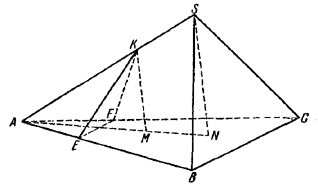

Мы считаем, что

^АE/_EB = ^АF/_FC= ¹/₂

Поэтому

^АE/_AB = ^АF/_AC= ¹/₃

и, следовательно,

S_{\(\Delta\)AEF} = ¹/₉S_{\(\Delta\)ABC} (1)

Пусть, далее, KMи SN -высоты пирамид KAEF и SABC. Легко видеть, что

^KM/_SN = ^АK/_AS= ²/₃

Поэтому KM = ²/₃SN и, учитывая (1), мы получаем, что

V_KAEF = ²/₂₇V_SABC

Искомое отношение равно ²/₂₇.