В правильной шестиугольной пирамиде через центр основания проведено сечение параллельно боковой грани. Найти отношение площади сечения к площади боковой грани.

Легко видеть, что в сечении получится равнобочная трапеция ABCD.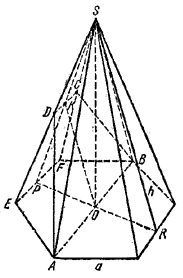

Пусть Р - середина стороны EF основания пирамиды. Рассмотрим \(\Delta\)SPR, содержащий высоту SO пирамиды. Отрезок KО, очевидно, является высотой трапеции ABCD.

Так как KO || SR, то KO =¹/₂ h, где h - апофема пирамиды.

Очевидно также, что АВ = 2а, где а - длина стороны основания пирамиды и DC = ¹/₂EF = ¹/₂ а . Поэтому

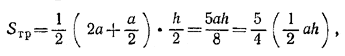
и, следовательно, искомое отношение равно ⁵/₄.